【笔记】最小项形式的逻辑函数

发表于 更新于 阅读次数：

前言

最小项形式的逻辑函数学习笔记

对比卡诺图

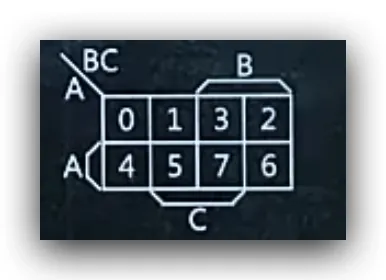
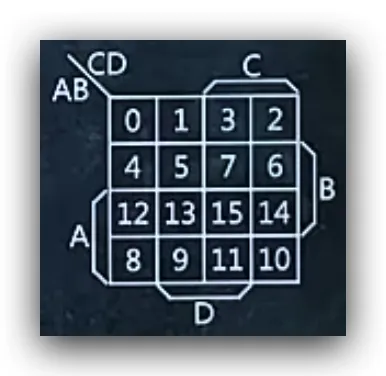
规律

  • 先将16个格填满0-15个数字

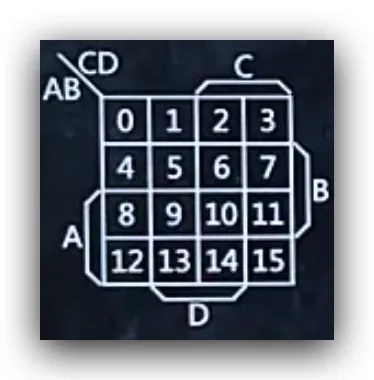
  • 然后将A区域的横行交换位置

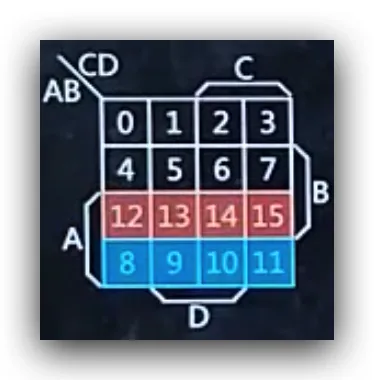
  • 然后将C区域的纵列交换位置

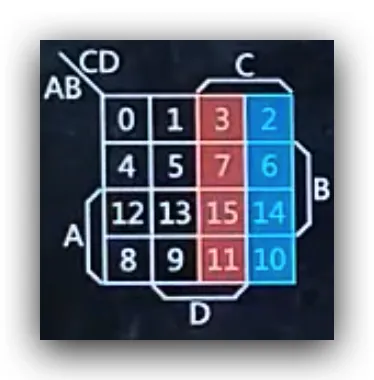
  • 最后得到的完整部分就是16个格的对比卡诺图
  • 最后得到的上半部分就是8个格的对比卡诺图

题型1

  • 用卡诺图法将逻辑函数变成最小项的形式

示例：用卡诺图法将逻辑函数 L=AB+BCD 变成最小项的形式

  1. 将函数表现在卡诺图里

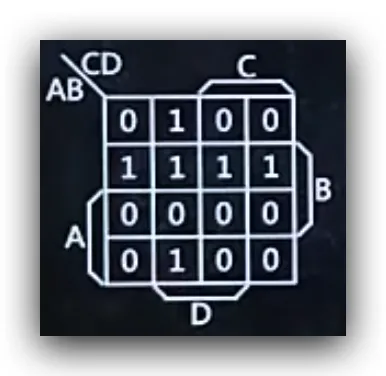
  1. 将题目卡诺图与对比卡诺图相对比

根据对比，找出题目卡诺图中为1的项，在对比卡诺图中找到对应项，得到结果用m数字表示


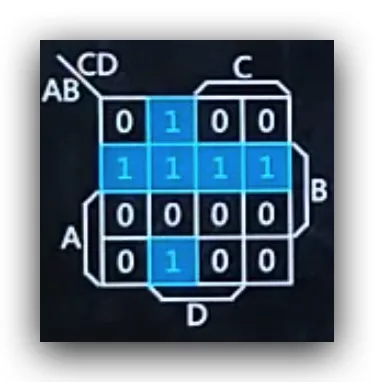
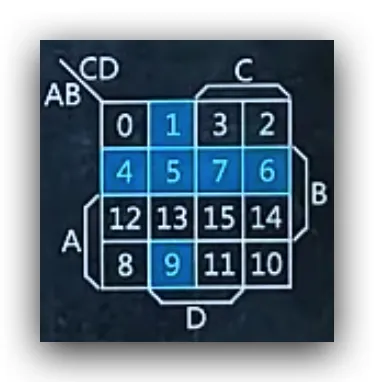
L=AB+BCD=m1+m4+m5+m7+m6+m9

题型2

  • 用公式法将逻辑函数变成最小项的形式

示例：用公式法将逻辑函数 L=AB+AC 变成最小项的形式

  1. 利用公式：A(B+B)=A，令每一项都包含A、B、C全部字母（或A、B、C、D全部字母），并化简为A、B、C的顺序（或A、B、C、D的顺序）

L=AB+AC
L=AB(C+C)+AC(B+B)
L=ABC+ABC+ACB+ACB
L=ABC+ABC+ABC+A BC

  1. 将A、B、C、D变成1，A、B、C、D变成0

111 110 011 001

  1. 将得到的数，由二进制数转换为十进制数

7 6 3 1

  1. 将得到的数字作为m的下标

∴ L=m7+m6+m3+m1

题型3

  • 将最小项的形式转换为变量的形式

示例：将 L(A,B,C)=m7+m6+m3+m1 转换为变量的形式

  1. 取出下标数字

7 6 3 1

  1. 将得到的数，由十进制数转换为二进制数，如果L(A,B,C)有三个字母，那就转化为3位二进制数（如果有四个字母，那就转化为4位二进制数）

111 110 011 001

  1. 第一位表示A、第二位表示B、第三位表示C（、第四位表示D），用或相连，得到一组逻辑函数
    • 如果该位上是1，就是这个字母本身
    • 如果该位上是0，就是这个字母的非

L=ABC+ABC+ABC+ABC

  1. 用卡诺图法或公式法化简逻辑函数

L=AB+AC

题型4

  • 将形如 L=Σm+Σd 的式子用卡诺图化简

示例：将 L(A,B,C,D)=Σm(1,4,5,6,7,9)+Σd(10,11,12,13,14,15) 用卡诺图化简

  1. 根据L(A,B,C,D)字母的个数，判断使用的是8个格的卡诺图还是16个格的卡诺图
  • 如果是3个字母，就是8个格的卡诺图
  • 如果是4个字母，就是16个格的卡诺图
  1. 在对比卡诺图中，将式子中m(1,4,5,6,7,9)位置的格子改为1，将式子中d(10,11,12,13,14,15)位置的格子改为×，将没有改动的位置的格子改为0

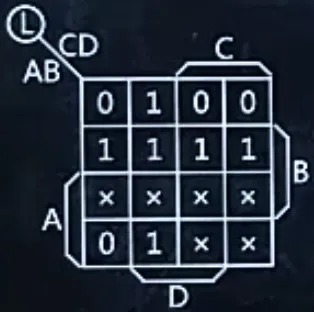
  1. 将×的位置看成1，寻找8个1（、4个1、2个1、1个1），将所有的1都表示完即可，而不需要表示完所有×，得到逻辑表达式

L=B+CD

完成

参考文献

哔哩哔哩——猴博士爱讲课